Making the good decision is the challenge that we often have. So, in this post, we will look at how applied machine learning classification can be used for the process of decision making.
The simple and quick approach to make decision is follow our past experience of similar situations. Usually we use compiling a list of pros and cons, asking someone for help or searching on the web. According to [1] we have two systems in our brain: logical and intuitive system:
“With every decision you take, every judgement you make, there is a battle in your mind – a battle between intuition and logic.”
“Most of the beliefs or opinions you have come from an automatic response. But then your logical mind invents a reason why you think or believe something.”
Most of the time our intuitive system is working efficiently, taking charge of all the thousands of decisions we make each day. But our intuitive system can be biased in many ways. For example it can be biased toward the latest unsuccessful outcome.
Besides this our memory can not remember a lot of information so we can not use efficiently all our past information and experience. That’s why people created tools like decision matrix that can help to improve decision making. In the next section we will look at techniques that facilitates using our rational decision making.

Decision Matrix
More advanced approach for making decision is score each possible option. In this approach we score each option against some criteria or feature. For example for the candidate product that we need to buy we are looking at price, quality, service and safety features. This approach results in creating decision matrix for analysis of possible options.
Below is an example of decision matrix [3] for choosing strategy for building some software project. Here we score 4 options based on the time to build and cost. The score is on the scale 0 (worst) – 100 (best). After we score each cell for time and cost rows, we can get sum of scores, rank and then make our choice (see last 3 rows)
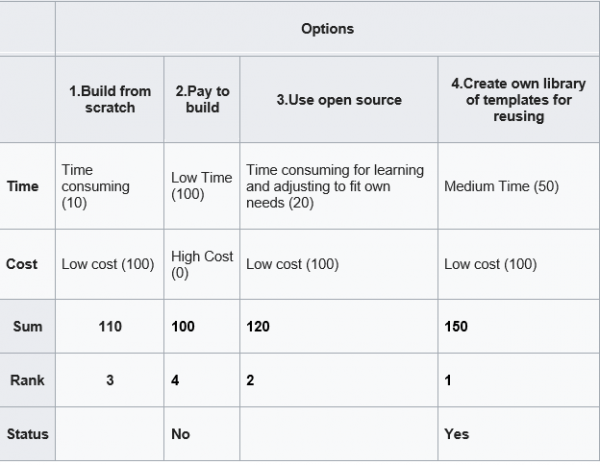
There are also other, similar to decision matrix tools: belief decision matrix[3], Pugh Matrix[4].
These tools allow do comparison analysis of available options vs features and this enforces our mind logically evaluate and rank as much as possible pros and cons based on some numerical metrics.
However there are some limitations also. Incorrect selection criteria will obviously lead to the wrong conclusion. Poorly defined criteria can have multiple interpretations. For example too low can mean different things. With many rows or columns it becomes labor intensive to fill out the matrix.
Machine Learning Approach for Making Decision
Machine learning techniques can also help us improve decision making and even solve some of the above limitations. For example with Feature Engineering we can evaluate what criteria are important for decision.
In machine learning making decision can be viewed as assigning or predicting correct label (for example buy, not buy) based on data for the item features. In the field of machine learning or AI this is known as classification problem.
Classification algorithms learn correct decisions from data. Below is the example of training data that we input to machine learning classification algorithm. (Xij represent some numerical values)
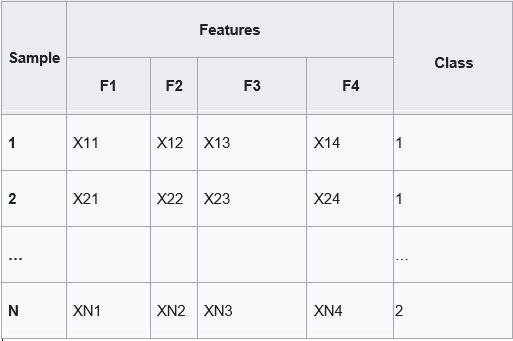
Our options (decisions) are now represented by class label (most right column), criteria are represented by features. So we now switched columns with rows. Using training data like above we train classifier and then use it to choose the class (make decision) for new data.
There are different classification algorithms such as decision tree, SVM, Naive Bayes, neural network classification. In this post we will look at classification with neural network.
We will use Keras neural network with 2 dense layers.
Per Keras documentation[5] Dense layer implements the operation:
output = activation(dot(input, kernel) + bias)
where activation is the element-wise activation function passed as the activation argument,
kernel is a weights matrix created by the layer,
and bias is a bias vector created by the layer (only applicable if use_bias is True).
So we can see that the dense layer is performing similar math that we were doing in decision matrix.
Python Source Code for Neural Network Classification Algorithms
Finally, below is the python source code for classification problem. To test this code we will use iris dataset. This dataset has 3 classes and 4 features. Our task here to make the classifier able to assign correct label class.
# -*- coding: utf-8 -*-
from keras.utils import to_categorical
from sklearn import datasets
iris = datasets.load_iris()
# Create feature matrix
X = iris.data
print (X)
# Create target vector
y = iris.target
y = to_categorical(y, num_classes=3)
print (y)
from sklearn.model_selection import train_test_split
x_train, x_test, y_train, y_test = train_test_split( X, y, test_size=0.33, random_state=42)
print (x_train)
print (y_train)
from keras.models import Sequential
from keras.layers import Dense
model = Sequential()
model.add(Dense(32, input_shape=(4,), activation='relu', name='L1'))
model.add(Dense(3, activation='softmax', name='L2'))
model.compile(optimizer='rmsprop',
loss='categorical_crossentropy',
metrics=['accuracy'])
print('Model Summary:')
print(model.summary())
model.fit(x_train, y_train, verbose=2, batch_size=10, epochs=100)
output = model.evaluate(x_test, y_test)
print('Final test loss: {:4f}'.format(output[0]))
print('Final test accuracy: {:4f}'.format(output[1]))
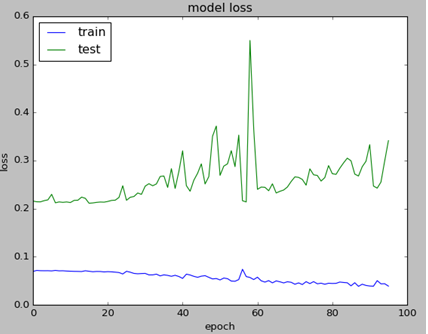
Below are results of neural network run.

As we can see our classifier is able to make correct decisions with 98% accuracy.
Thus we investigated different approaches for making decision. We saw how machine learning can be applied to this too. Specifically we looked at neural network classification algorithm for selecting correct label.
I would love to hear what types of decision making tools do you use for making decisions? Also feel free to provide feedback or suggestions.
References
1. How do we really make decisions?
2. What Is a Decision Matrix? Definition and Examples
3. Decision matrix From Wikipedia, the free encyclopedia
4. The Systems Engineering Tool Box
5. Keras Documentation








You must be logged in to post a comment.